Los números racionales son los que se pueden representar por medio de fracciones.
Los números racionales representan partes de algo que se ha dividido en partes iguales. Por ejemplo, si cortamos una tarta en 4 trozos iguales y nos tomamos tres trozos de la tarta nos hemos comido 3/4 de la tarta.
Son números racionales 1/2, 3/4, 11/5, 2535/3, ... También son números racionales los números enteros 2 = 2/1, 5 = 10/2, ...
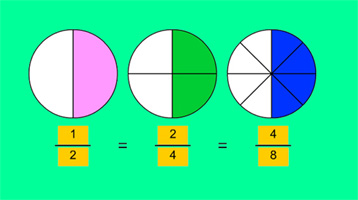
Un mismo número racional se puede expresar con varias fracciones.
Por ejemplo: 1/2, se puede expresar como 1/2, 2/4, 3/6, ... De todas estas formas, la primera se llama
fracción irreducible y las demás fracciones equivalentes.
Hay infinitos números racionales. Aunque parezca increíble, podemos 'contar' (asociar un número natural a cada número racional) los números racionales.
Muchas veces los números racionales se expresan como números decimales. Por ejemplo: 1/2 = 0,5, 3/4 = 0,75.
Limitados y periódicos. Estos últimos se pueden clasificar a su vez, en periódicos puros y periódicos mixtos.
 Los números racionales limitados son los que en su representación decimal tienen un número fijo de números. Por ejemplo: 1/4 = 0,25.
Los números racionales limitados son los que en su representación decimal tienen un número fijo de números. Por ejemplo: 1/4 = 0,25.Los números racionales periódicos son los que en su representación decimal tienen un número ilimitado de números.
Hay dos tipos de números racionales periódicos: Los periódicos puros: Un número, o grupo de números, se repite ilimitadamente, desde el primer decimal. (por ejemplo: 3,838383...) y los periódicos mixtos: un número o grupo de números se repite ilimitadamente a partir del segundo o posterior decimal (por ejemplo 3,27838383...).
ENSEÑANZA DE LOS NÚMEROS RACIONALES
Los estudiantes en primaria manipulan las fracciones, las representan gráficamente, las ubican en la recta numérica y las escriben en notación decimal, además, conocen la noción de fracciones equivalentes. Todos estos conocimientos, que ya posee el estudiante, permiten abordar el concepto de número racional positivo con los cuadros gráfico y numérico. 
En el cuadro gráfico, se puede partir del hecho que dos fracciones son equivalentes si representan la misma cantidad. La idea es que antes de introducir los racionales, el estudiante manipule correctamente las fracciones. Así, se inicia considerando la fracción  con
con  y
y  enteros positivos, como la porción que se
enteros positivos, como la porción que se
obtiene al dividir cada unidad en  partes y tomar
partes y tomar  de esas partes.
de esas partes. 
Qué novedades traen
eso que enseñar fracciones es adentrarse en cuestiones matemáticas complejas que van más allá de pintar pedacitos de un dibujo.
Los que enseñamos matemática sabemos que el conjunto Q de los números racionales es denso y que esto quiere decir que entre dos racionales siempre es posible encontrar uno más.
Esta cuestión es la más importante, me parece, al comenzar a enseñar las fracciones porque los estudiantes pequeños que vienen de construir la idea de que los números naturales son tan grandes como se quiera, o sea el infinito hacia afuera por así decirlo, con las fracciones se enfrentan al infinito hacia adentro ya que con las fracciones se puede partir en tantos pedacitos iguales como se quiera. Con números naturales agrego y agrego y siempre es posible encontrar un número natural mayor; con las fracciones tengo una cantidad y parto y parto y siempre es posible obtener una cantidad mayor de pedacitos cada vez más chicos, claro.
Si a los alumnos se le plantean actividades del tipo de las que proponemos o de las muchas diferentes que se pueden proponer, se nota una mejoría considerable no sólo en los resultados sino también en la aceptación de los alumnos a la materia.




ummmmm q, creo que `rimera que no entendi ni un poquiito
ResponderEliminarcuales son las aplicaciones de los nuemro irracionales en la vida adiaria
ResponderEliminarx2
Eliminar